1. 边缘检测#

1.1 形成边缘的原因#

照明不连续
深度不连续
反射属性(材质)不连续
法向不连续

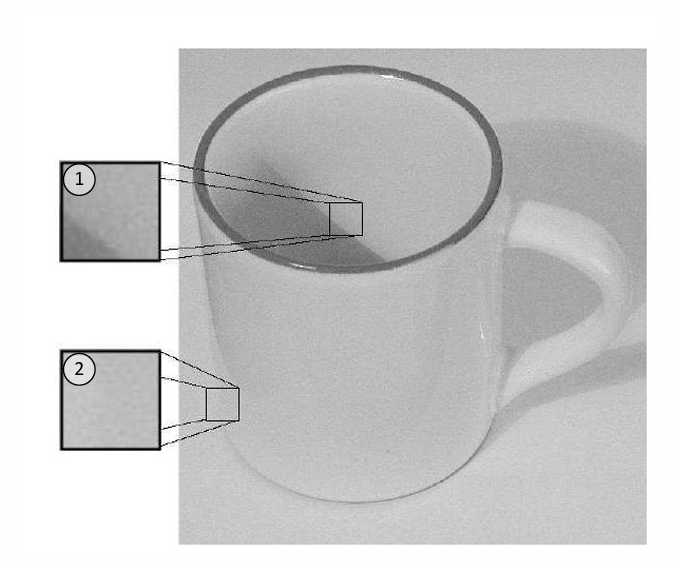
但是图片中的边缘有时也不能很好地反映事物的外形。比如因为光照不连续产生的边缘①其实并非杯子本身的形状。
也有的边缘会因为物理世界的复杂性而丢失，比如②分不清杯子和桌板。

1.2 边缘检测与差分算子#

1.2.1 边缘模型#

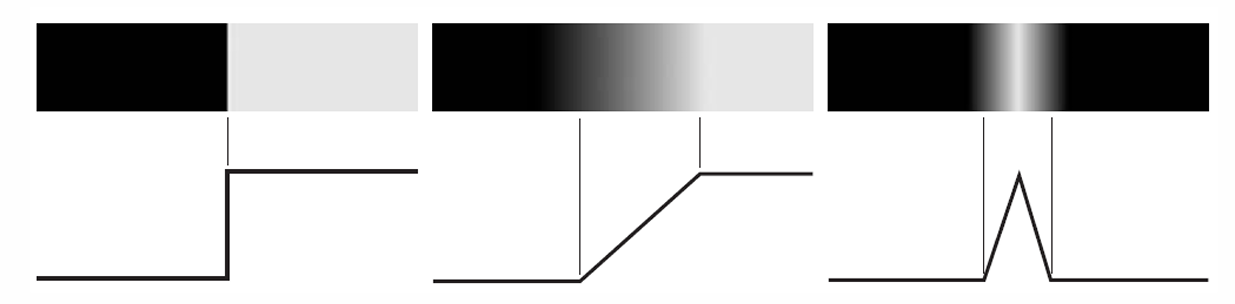
理想的边缘有3种:

阶跃边缘(Step Edge)
斜坡边缘(Ramp Edge)
屋脊边缘(Ridge Edge)

1.2.2 差分算子#

边缘就是一张图像中两边亮度值相差(变化)非常大的区域，可以把检测边缘和求一幅图像的导函数(变化率)联系起来。把一阶导函数取到极大值或者极小值(负数，非零)的点作为边缘，对应在二阶导数的零点。

而离散图像的导函数即差分。把差分图像作为导数图像。

一般有3种差分方式：

\begin{align} &1. 前向差分: \Delta f(x) = f(x+1) -f(x)\\ &2. 后向差分: \Delta f(x) = f(x) -f(x-1)\\ &3. 中心差分: \Delta f(x) = \frac{1}{2}(f(x+1) -f(x-1)) \end{align}

据说是中心差分性能好于其他差分方式。

由于卷积运算可以表示 $f(x)$ 邻域内的线性运算，因此这三种差分方式可以用卷积核来完成:

差分方式	公式	kernel
前向差分	$\Delta f(x) = f(x+1) -f(x)$	$[1,-1,0]$
后向差分	$\Delta f(x) = f(x) -f(x-1)$	$[0,1,-1]$
中心差分	$\Delta f(x) = \frac{1}{2}(f(x+1) -f(x-1))$	$\frac{1}{2}[1,0,-1]$
二阶中心差分	$f''(x) = f(x+1) - 2f(x)+f(x-1)$	$[1,-2,1]$ ：Laplacian卷积核

由于图像的噪声也对应了图像上变化很大的部分，因此一般在使用差分算子前会对图像做一次平滑。比如高斯平滑，均值平滑。
如果拉普拉斯卷积核前使用了高斯核平滑，则合在一起就成为高斯拉普拉斯卷积核LoG(Laplace of Gauss)。

1.3 一阶差分算子检测图像边缘#

1.3.1 边缘检测一般步骤#

对于一维情形，差分算子形如 $[1,0,-1]$ ，需要在之前进行一次平滑，如果采用均值平滑 $[1,1,1]^T$ ,则得到 $Prewitt$ 卷积算子:

Prewitt_x = [1,1,1]^T\times[1,0,-1] = \left[\begin{matrix}1,0,-1 \\1,0,-1\\1,0,-1 \end{matrix}\right]

另一种得到这个算子的角度是: 做水平方向的差分时，平均上下两行会让结果更加准确一些。

而这只是得到了水平方向的梯度 $G_x$ ，竖直方向的梯度 $G_y$ 可以通过竖直的卷积算子(水平算子的转置)得到。

Prewitt_y =\left[\begin{matrix}&1,&1,&1 \\&0,&0,&0\\&-1,&-1,&-1 \end{matrix}\right]

得到梯度 $G = \left[\begin{matrix}G_x \\ G_y\end{matrix}\right]$ 。

梯度模长 $|G|$ 和方向 $d$ ：

|G| = \sqrt{G_x^2+G_y^2} 或者|G_x|+|G_y|\\ d=arctan(\frac{G_y}{G_x})

所以检测边缘的一般步骤是:

\begin{align} &0. 对原图进行平滑滤波降噪\\ &1. 用kernel_x求水平梯度G_x和用kernel_y求竖直梯度G_y \\ &2. 求平方和的根或者是近似得到梯度幅度M，得到梯度幅度图像G'\\ &3. 二值化梯度幅度图像G'，threshold = M \end{align}

1.3.2 常用的一阶微分算子#

常用的一阶差分算子有 $Prewitt,Sobel$ 算子。

算子	$kernel_x$
3*3 $Prewitt_x$	$\left[\begin{matrix}1,0,-1 \\1,0,-1\\1,0,-1 \end{matrix}\right]$
3*3 $Sobel_x$	$\left[\begin{matrix}1,0,-1 \\2,0,-2\\1,0,-1 \end{matrix}\right]$
5*5 $Sobel_x$	$\left[\begin{matrix}1,2,0,-2,-1 \\2,3,0,-3,-2\\3,5,0,-5,-3 \\2,3,0,-3,-2\\ 1,2,0,-2,-1\end{matrix}\right]$

注意: 这些卷积核已经自带了一部分的平滑效果。
当卷积核的大小变大以后，平滑滤波的效果变强，但是对于边缘的定位精确性会减弱。

1.4 二阶差分算子检测图像边缘#

二阶方向导数 $\frac{\partial^2 f}{\partial \vec{l}^2}$ :

\begin{align} \frac{\partial^2 f}{\partial \vec{l}^2}=\frac{f'_{\vec{l}}}{\partial \vec{l}} &= \frac{f'_xcos\theta+f'_ysin\theta}{\partial \vec{l}} \\ &=f''_{xx}cos^2\theta + f''_{xy}cos\theta sin\theta + f''_{yx}sin\theta cos\theta+f''_{yy}sin^2\theta \end{align}

在 $Laplace$ 算子里就近似为:

|\frac{\partial^2 f}{\partial \vec{l}^2}|_{max} \approx f''_{xx} + f''_{yy}| \\ |\nabla^2 f| \approx [f(x+1,y) - 2*f(x,y) + f(x-1,y)] + [f(x,y+1) - 2*f(x,y) + f(x,y-1)]

由于 $f(x,y)$ 邻域内的线性运算都可以转化为卷积运算，因此有 $Laplace$ 卷积核:

Laplace=\left[\begin{matrix}&0,&1,&0 \\ &1,&-4,&1 \\ &0,&1,&0\end{matrix}\right]

$Laplace$ 算子是旋转对称的，因此具有旋转不变性(90°)。

因为边缘对应的是一阶导数的极大值点，也就是二阶导数的零点。需要把 $Laplace$ 算子卷积得到的结果找出过0点的位置。
$Laplace$ 算子卷积得到的结果已经是幅度值！

1.5 Canny边缘检测#

$Canny$ 检测的准则是:

检漏率低、正确率高
检测到的相应尽量在真实边缘的中心位置
对单一边缘的响应只有一个边缘点

$Canny$ 边缘检测的核心思想是:
非极大值抑制(找到中心位置，单一相应点)
延迟阈值(防止错检、漏检)

1.5.0 得到梯度图像 $G$ #

和一般一阶差分检测边缘的方法一样， $Canny$ 方法也先用某个核(比如Sobel)得到一张梯度图 $G$ 。既有梯度模长也有梯度方向。接着进行非极大值抑制和延迟阈值。

1.5.1 非极大值抑制#

在梯度图 $G$ 上对每一点 $(x,y)$ 沿着梯度方向 $d$ 的邻域进行搜索，并且抑制掉那些比 $(x,y)$ 小的点。只留下某一区域内的极大值点。

一定程度上可以保证检测到的点会是单一边缘的单一响应。并且大概率在中心位置。

1.5.2 延迟阈值#

二值化时的 $threshold$ 很难确定，如果太大会导致漏检，如果太小则会导致错检(边缘精确性不高)。
图像上的边缘分布大概率是有空间局部性特征的。所以 $Canny$ 采用延迟阈值+边缘连接的手段来解决这个问题。

设定两个大小不一样的 $Hi,Lo，Hi > Lo$ ，用 $Hi$ 得到强边缘图，而用 $Lo$ 得到弱边缘图。

强边缘几乎已经可以确定是真实地边缘，而弱边缘却还需要观察。

1.5.3 边缘连接#

边缘点和边缘点分布在一起的可能性比较大。
因此，如果一个弱边缘点周边有强边缘点，那它大概率是边缘点。但如果它周边一个强边缘点都没有，那它大概率不是边缘点。

按照如上规则删去或者保留弱边缘点，得到最后检测地结果。

1.6 边缘检测的尺度#

由于平滑操作对于细节来说有模糊的作用，图像越平滑细节也会越少。这会导致图像中的某些细小边缘会逐渐消失。

可以对图像施以一系列 $\sigma$ 不同的高斯滤波用来提取不同尺度的边缘特征。

1.7 边缘检测和模式匹配: 轮廓匹配#

物体 $A$ 的轮廓(边缘信息)，可以用来在一张图像 $G$ 上识别物体 $A$ 。

提取 $G$ 的边缘图 $G'$ 。